爬虫协议

题目

小蓝同学在开发网站时了解到了一个爬虫协议，该协议指网站可建立一个特别的txt文件来告诉搜索引擎哪些页面可以抓取，哪些页面不能抓取，而搜索引擎则通过读取该txt文件来识别这个页面是否允许被抓取。爬虫协议并不是一个规范，而只是约定俗成的，所以并不能保证网站的隐私。

题目界面

无\找不到

题解

https://example.com/ robots.txt 查看敏感路径。属于web方向的签到题，签到等于送分

流量分析

题目

wireshark在手，简单的数据包分析就是小case。

题目界面

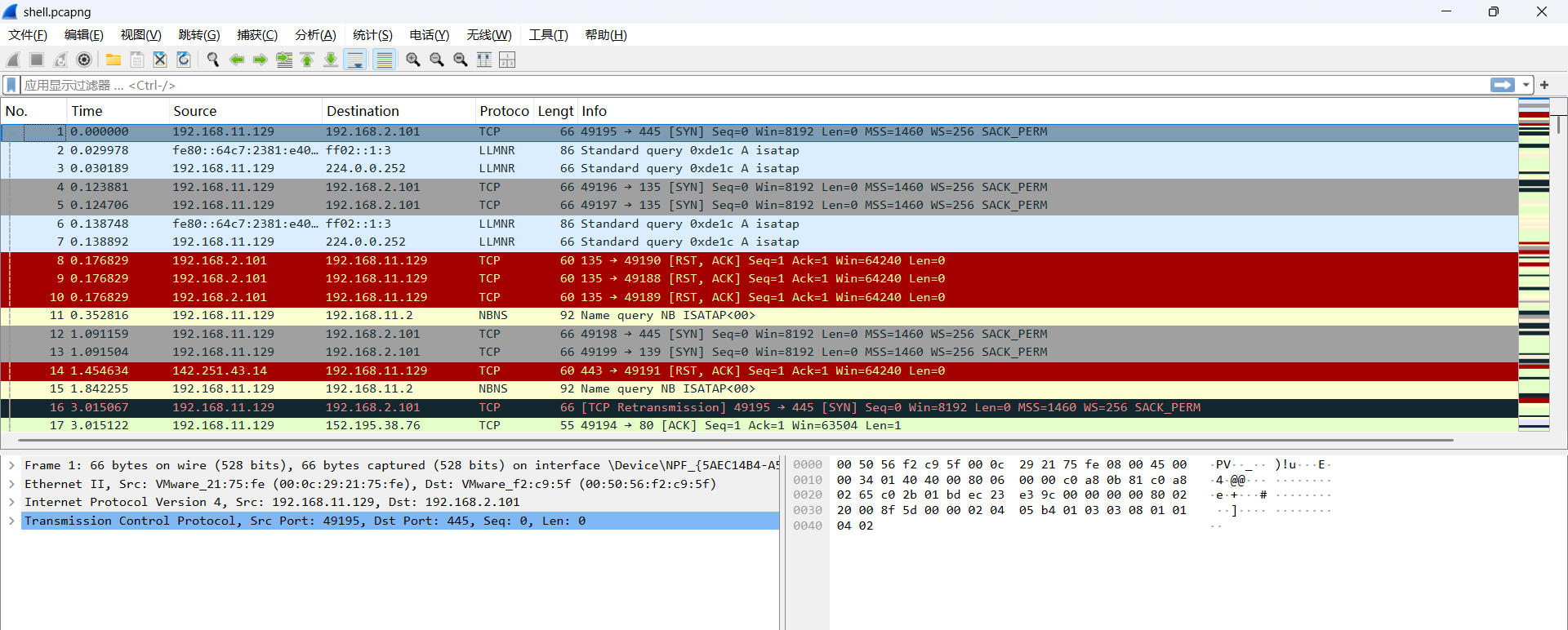
题解

打开题目给的数据包，这题很简单，简直是送分的。直接搜索flag就好了。Misc方向的签到题。
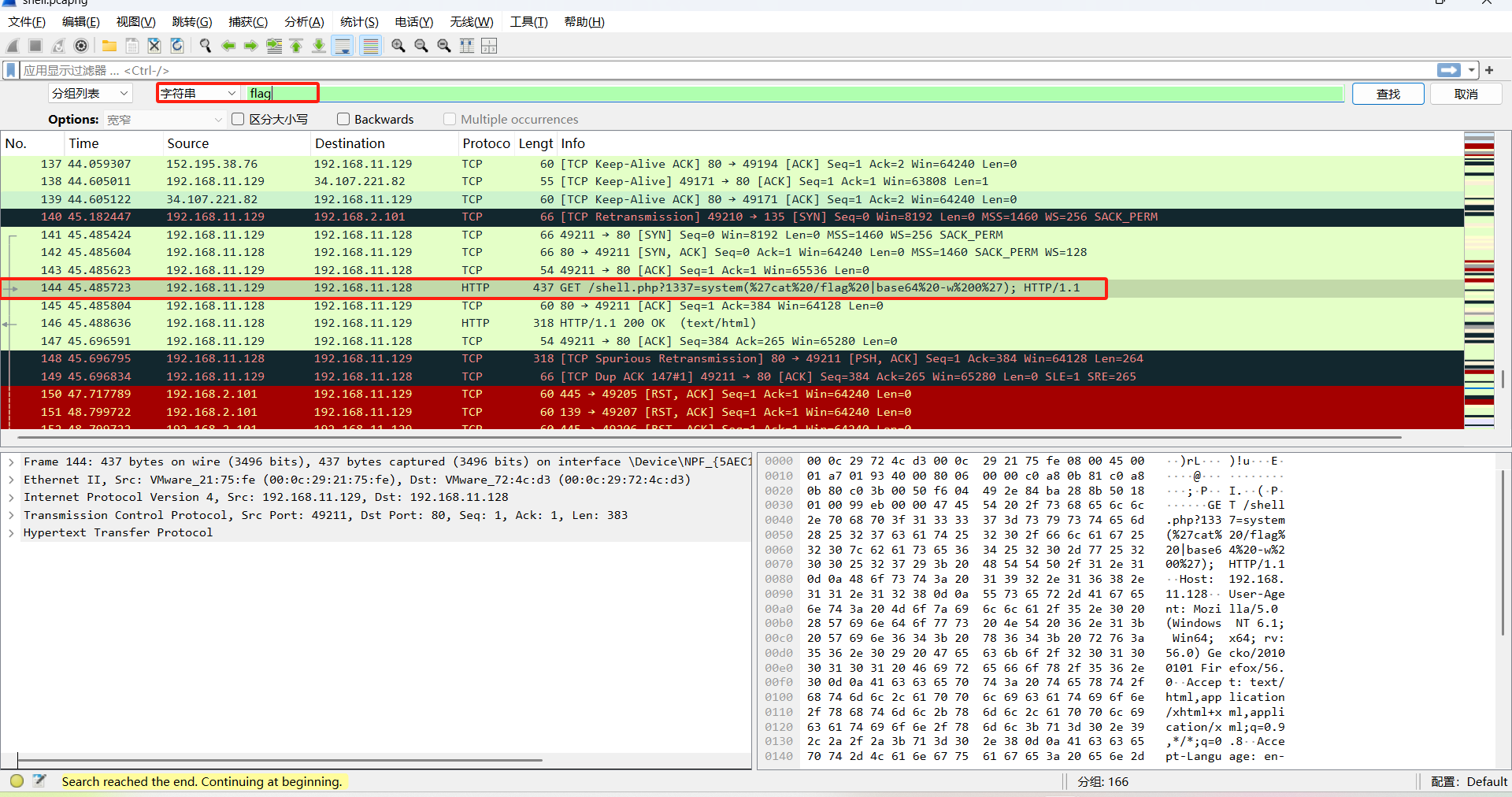找到flag字符串。追踪流查看一下。

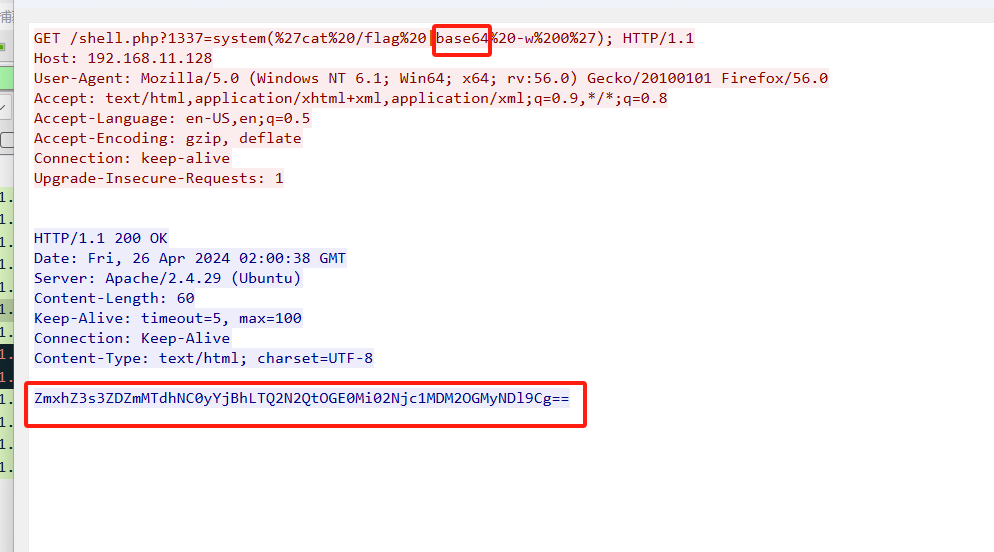
一眼base64加密。我们解码一下就可以得出flag了。
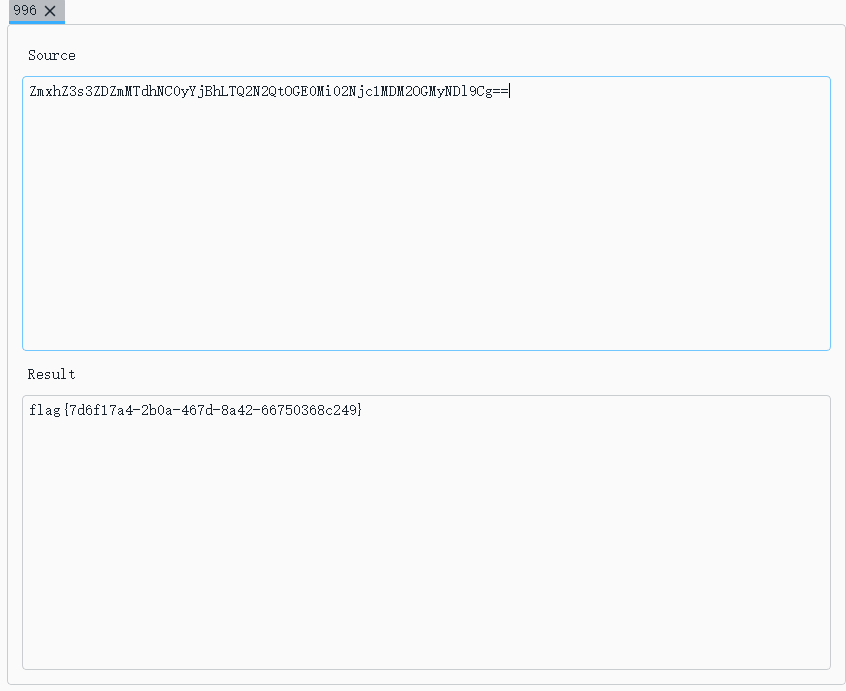得出flag。

AES加密

题目

CyberChef是一个用于加密、编码、压缩和数据分析的网络应用程序，被称为“网络版瑞士军刀”，旨在使技术和非技术分析人员能够以复杂的方式操作数据，而无需处理复杂的工具或算法。

题目界面

题解

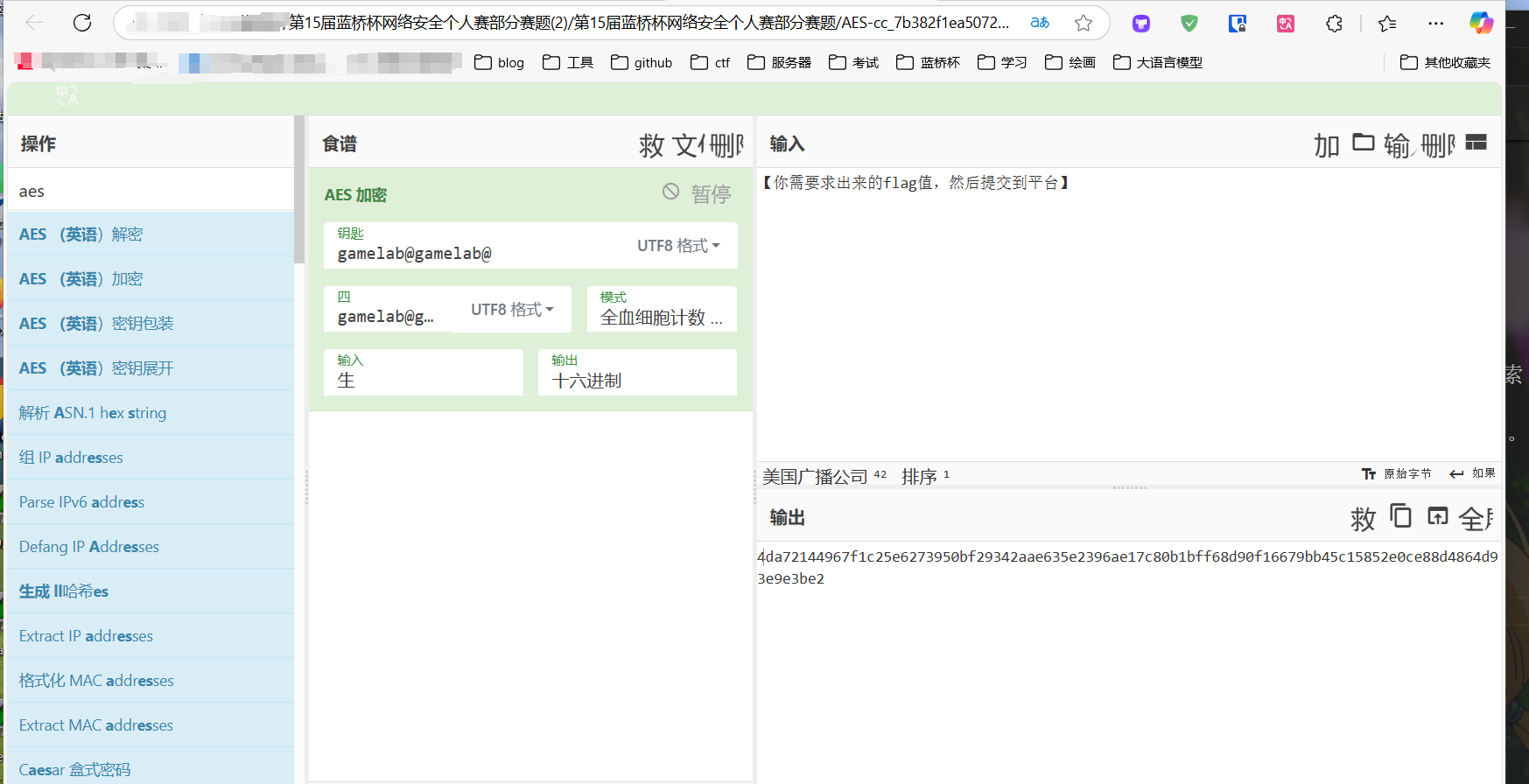
题目提示的很明显，是使用CyberChef加密的AES。我们使用工具解密。告诉我们加密的结果是“4da72144967f1c25e6273950bf29342aae635e2396ae17c80b1bff68d90f16679bb45c15852e0ce88d4864d93e9e3be2”
密钥是“gamelab@gamelab@”，初始向量“gamelab@gamelab@”，模式是“CBC”（密码块链模式）
Input（输入）：这是要加密的数据。在图片中，输入数据是原始文本（Raw）。
Output（输出）：这是加密后的数据。在图片中，输出数据是以十六进制（Hex）格式表示的。
UTF8：这表示输入和IV的编码格式是UTF-8，这是一种常用的字符编码方式。
好知道这些，我们用工具解密就好了
得出flag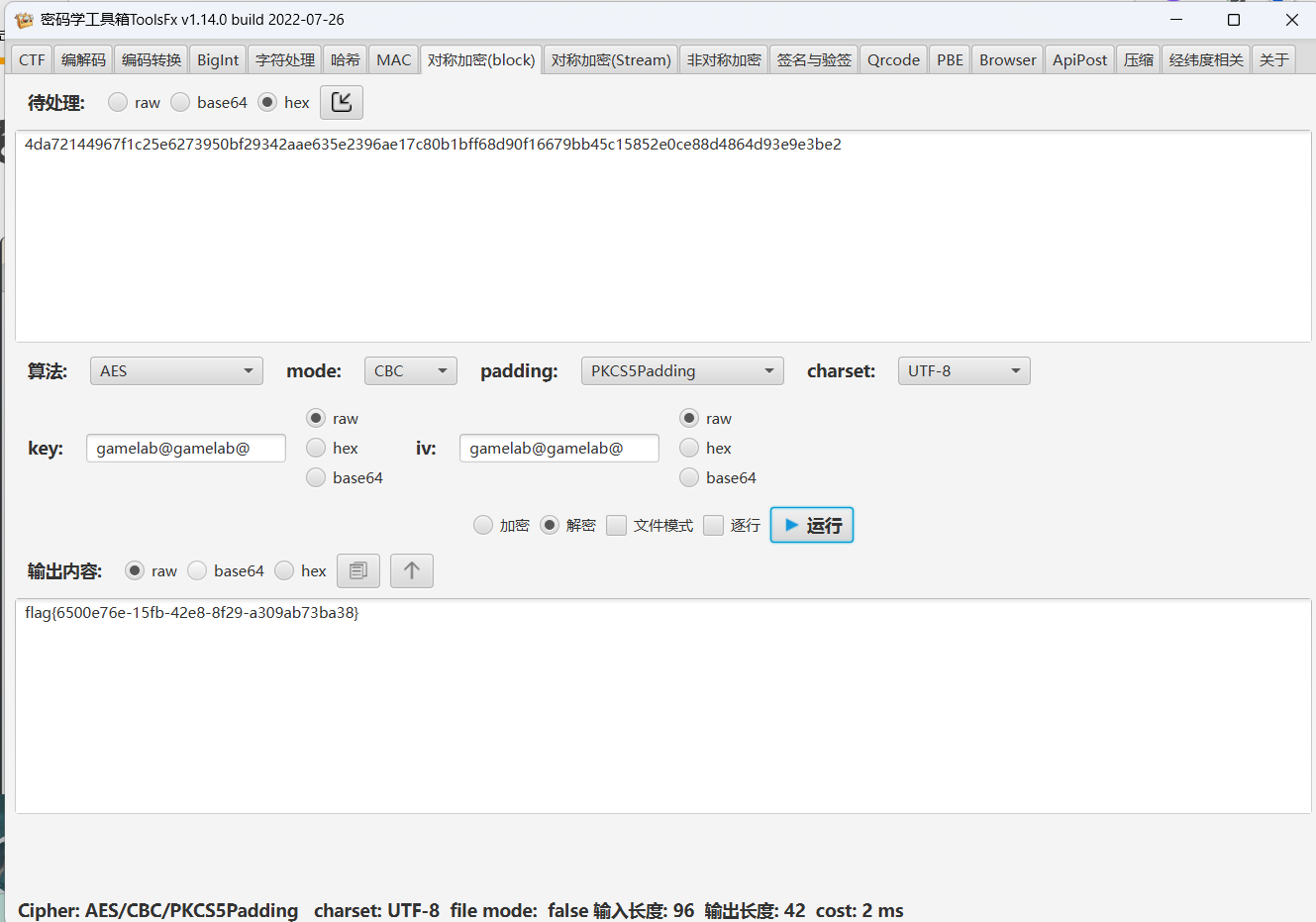

RSA加密

题目

模运算在密码学中是一种常见的加密手段，而中国剩余定理则提供了一种解密的方法。小蓝同学运用这个定理来获得c，进而获得了flag。

题目界面

打开task.py文件

from Crypto.Util.number import *
from gmpy2 import *
flag = b'xxx'

//bytes_to_long函数将flag转换为长整型
def bytes_to_long(flag):
    pass


m =  bytes_to_long(flag)
p = getPrime(512) //生成一个512位的素数
q = next_prime(p) //p后面下一个素数
e = 65537 //公钥指数
n = p * q //RSA数模
phi = (p - 1) * (q - 1) //欧拉函数
d = inverse(e, phi) //私钥指数
d1 = d % q //q的模
d2 = d % p //p的模
c = pow(m, e, n) //计算c为m的e次方的模n

print(n)
print(d1)
print(d2)
print(c)


# 94581028682900113123648734937784634645486813867065294159875516514520556881461611966096883566806571691879115766917833117123695776131443081658364855087575006641022211136751071900710589699171982563753011439999297865781908255529833932820965169382130385236359802696280004495552191520878864368741633686036192501791 //n
# 4218387668018915625720266396593862419917073471510522718205354605765842130260156168132376152403329034145938741283222306099114824746204800218811277063324566
# 9600627113582853774131075212313403348273644858279673841760714353580493485117716382652419880115319186763984899736188607228846934836782353387850747253170850
# 36423517465893675519815622861961872192784685202298519340922692662559402449554596309518386263035128551037586034375613936036935256444185038640625700728791201299960866688949056632874866621825012134973285965672502404517179243752689740766636653543223559495428281042737266438408338914031484466542505299050233075829 //c

题解

密码方向的签到题，密码方面的这题感觉没有前面两题那里那么送分了。
好好好，其实就是一个python写的RSE加密的代码罢了。
我们知道n,但是不知道p和q，我们用yafu来解。
解出了p和q。
p="9725277820345294029015692786209306694836079927617586357442724339468673996231042839233529246844794558371350733017150605931603344334330882328076640690156923"
q="9725277820345294029015692786209306694836079927617586357442724339468673996231042839233529246844794558371350733017150605931603344334330882328076640690156717"
知道了n，p，q我们用工具来计算d。

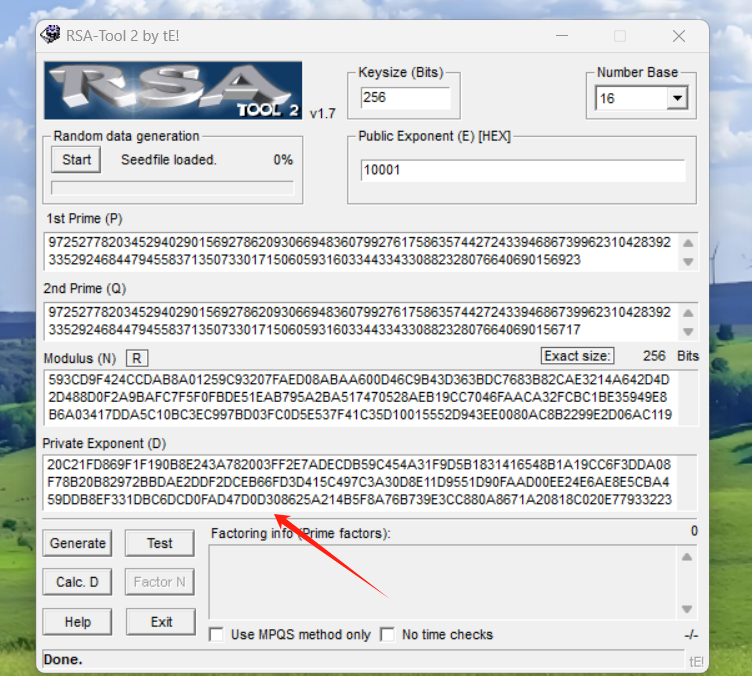
d="78306401213576455103059040812429532567314868248881744069988640402793619121841205201343010853943948914374488022231130886905591235682013238487920976502614077619584602780243299701688747389155885229684676681475966133830981320544832967668594175322039872222094518139655553698596307648015014710172433906454004750433"
好，题目给了你n,c,我们又用工具解出了d。M=pow(c,d,n)

# 假设你已经有了以下值
C = 36423517465893675519815622861961872192784685202298519340922692662559402449554596309518386263035128551037586034375613936036935256444185038640625700728791201299960866688949056632874866621825012134973285965672502404517179243752689740766636653543223559495428281042737266438408338914031484466542505299050233075829   # 替换为实际的密文
N = 94581028682900113123648734937784634645486813867065294159875516514520556881461611966096883566806571691879115766917833117123695776131443081658364855087575006641022211136751071900710589699171982563753011439999297865781908255529833932820965169382130385236359802696280004495552191520878864368741633686036192501791  # 替换为实际的模数
d = 78306401213576455103059040812429532567314868248881744069988640402793619121841205201343010853943948914374488022231130886905591235682013238487920976502614077619584602780243299701688747389155885229684676681475966133830981320544832967668594175322039872222094518139655553698596307648015014710172433906454004750433  # 替换为实际的私有指数

# 解密过程
M = pow(C, d, N)
print("Decrypted message:", M)

我们写一串简单的代码，得到
但是这个是数字。56006392793405651484479522122206171623656223206491196256547969652307343321460437326127016915766960509
我们是要找flag的嘛。所以利用工具
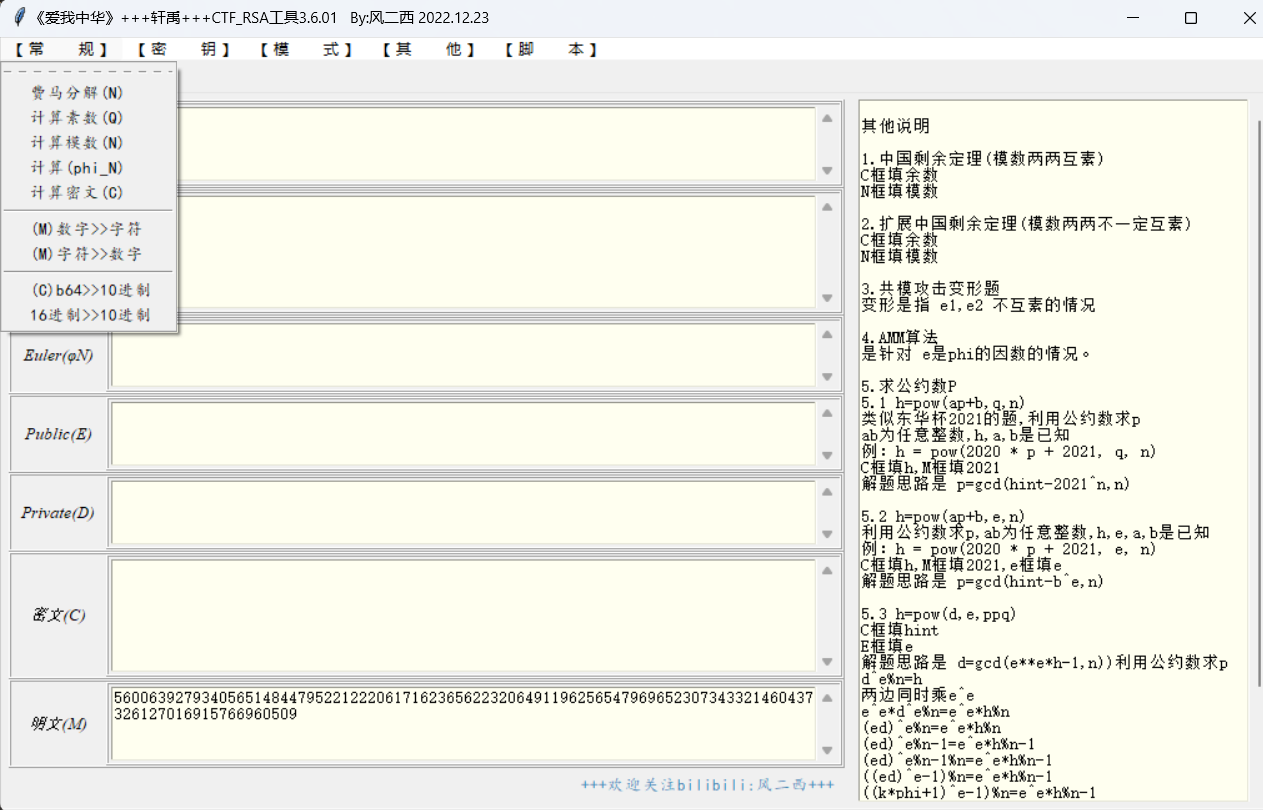选择数字转字符。
得到flag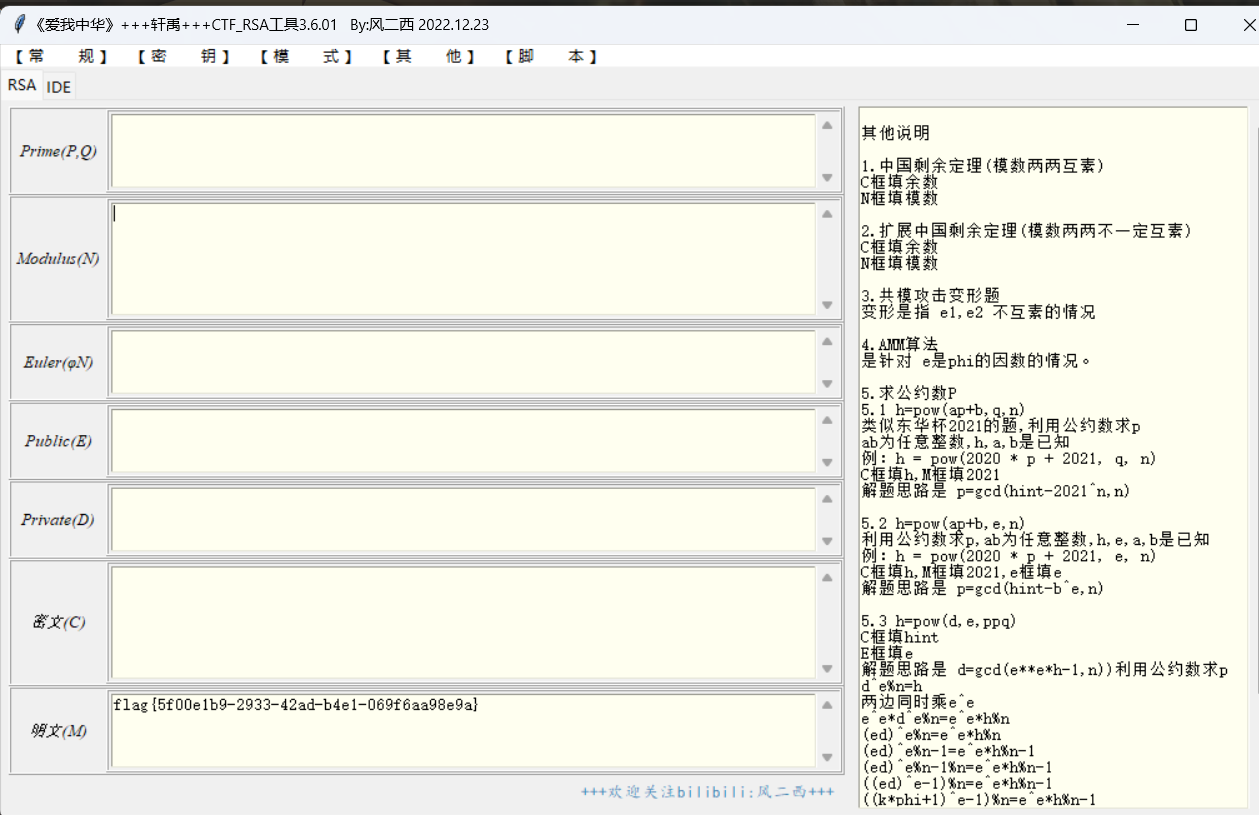
flag{5f00e1b9-2933-42ad-b4e1-069f6aa98e9a}

DWT盲水印

题目

题目内容：随着数字技术的迅猛发展，图像在网络上的传播日益广泛。然而，这也带来了版权保护、信息认证和内容完整性验证等一系列问题。数字水印技术作为一种有效的信息隐藏和认证手段，请分析出图片中隐藏的信息。

题目界面

orign文件里有密码字典文件。不全、orign压缩包和newlmg.png图片文件以及lose.py的脚本文件
lose.py脚本文件

class WaterMarkDWT:
    def __init__(self, origin: str, watermark: str, key: int, weight: list):
        self.key = key
        self.img = cv2.imread(origin)
        self.mark = cv2.imread(watermark)
        self.coef = weight
 

    def arnold(self, img):
        r, c = img.shape
        p = np.zeros((r, c), np.uint8)
 
        a, b = 1, 1
        for k in range(self.key):
            for i in range(r):
                for j in range(c):  
                    x = (i + b * j) % r
                    y = (a * i + (a * b + 1) * j) % c
                    p[x, y] = img[i, j]
        return p
 
    def deArnold(self, img):
        r, c = img.shape
        p = np.zeros((r, c), np.uint8)
 
        a, b = 1, 1
        for k in range(self.key):
            for i in range(r):
                for j in range(c): 
                        x = ((a * b + 1) * i - b * j) % r
                        y = (-a * i + j) % c
                    p[x, y] = img[i, j]
        return p
 

 
    def get(self, size: tuple = (1200, 1200), flag: int = None):
        img = cv2.resize(self.img, size)
 
        img1 = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
        img2 = cv2.cvtColor(self.mark, cv2.COLOR_RGB2GRAY)
 
        c = pywt.wavedec2(img2, 'db2', level=3)
        [cl, (cH3, cV3, cD3), (cH2, cV2, cD2), (cH1, cV1, cD1)] = c
 
        d = pywt.wavedec2(img1, 'db2', level=3)
        [dl, (dH3, dV3, dD3), (dH2, dV2, dD2), (dH1, dV1, dD1)] = d
 
        a1, a2, a3, a4 = self.coef
 
        ca1 = (cl - dl) * a1
        ch1 = (cH3 - dH3) * a2
        cv1 = (cV3 - dV3) * a3
        cd1 = (cD3 - dD3) * a4
 
        waterImg = pywt.waverec2([ca1, (ch1, cv1, cd1)], 'db2')
        waterImg = np.array(waterImg, np.uint8)
 
        waterImg = self.deArnold(waterImg)
 
        kernel = np.ones((3, 3), np.uint8)
        if flag == 0:
            waterImg = cv2.erode(waterImg, kernel)
        elif flag == 1:
            waterImg = cv2.dilate(waterImg, kernel)
 
        cv2.imwrite('水印.png', waterImg)
        return waterImg


if __name__ == '__main__':
    img = 'a.png'
    k = 20
    xs = [0.2, 0.2, 0.5, 0.4]
    W1 = WaterMarkDWT(img, waterImg, k, xs)

题解

我们先利用密码字典，把orign.zip的压缩包的密码破解出来。

先利用Winscp把这个工具把字典文件和orign.zip文件传到kali里面。因为Kali里面可以下载fcrackzip的工具。至于为什么不直接用John the Ripper，是因为John the Ripper破解orign.zip文件时。提示文件或者文件名用了非utf-8编码，破解不了。所以用fcrackzip。
fcrackzip这个工具也不行，只能破解出可能的密码。一个一个的去试太麻烦了。
这两工具都不行了，经过检索找到ARCHPR爆破工具。

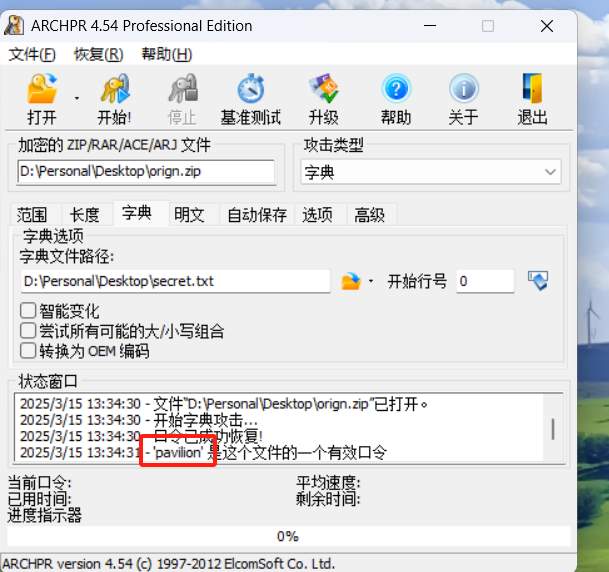
破解成功。使用这个工具，把orign.zip解压出来。得到a.png。

现在只需要改一下lose.py的代码，就可以得到水印了。

import cv2
import numpy as np
import pywt


class WaterMarkDWT:
    def __init__(self, origin: str, watermark: str, key: int, weight: list):
        self.key = key
        self.img = cv2.imread(origin)
        self.mark = cv2.imread(watermark)
        self.coef = weight

    def arnold(self, img):
        r, c = img.shape
        p = np.zeros((r, c), np.uint8)

        a, b = 1, 1
        for k in range(self.key):
            for i in range(r):
                for j in range(c):
                    x = (i + b * j) % r
                    y = (a * i + (a * b + 1) * j) % c
                    p[x, y] = img[i, j]
        return p

    def deArnold(self, img):
        r, c = img.shape
        p = np.zeros((r, c), np.uint8)

        a, b = 1, 1
        for k in range(self.key):
            for i in range(r):
                for j in range(c):
                    x = ((a * b + 1) * i - b * j) % r
                    y = (-a * i + j) % c
                    p[x, y] = img[i, j]
        return p

    def get(self, size: tuple = (1200, 1200), flag: int = None):
        img = cv2.resize(self.img, size)

        img1 = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
        img2 = cv2.cvtColor(self.mark, cv2.COLOR_RGB2GRAY)

        c = pywt.wavedec2(img2, 'db2', level=3)
        [cl, (cH3, cV3, cD3), (cH2, cV2, cD2), (cH1, cV1, cD1)] = c

        d = pywt.wavedec2(img1, 'db2', level=3)
        [dl, (dH3, dV3, dD3), (dH2, dV2, dD2), (dH1, dV1, dD1)] = d

        a1, a2, a3, a4 = self.coef

        ca1 = (cl - dl) * a1
        ch1 = (cH3 - dH3) * a2
        cv1 = (cV3 - dV3) * a3
        cd1 = (cD3 - dD3) * a4

        # Ensure all coefficients have the same shape
        ca1 = cv2.resize(ca1, (cD3.shape[1], cD3.shape[0]))

        waterImg = pywt.waverec2([ca1, (ch1, cv1, cd1)], 'db2')
        waterImg = np.array(waterImg, np.uint8)

        waterImg = self.deArnold(waterImg)

        kernel = np.ones((3, 3), np.uint8)
        if flag == 0:
            waterImg = cv2.erode(waterImg, kernel)
        elif flag == 1:
            waterImg = cv2.dilate(waterImg, kernel)

        return waterImg


if __name__ == '__main__':
    img = 'a.png'
    watermark = 'newImg.png'
    
    k = 20
    xs = [0.2, 0.2, 0.5, 0.4]
    
    W1 = WaterMarkDWT(img, watermark, k, xs)
    extracted_watermark = W1.get()
    cv2.imwrite('提取出的水印.png', extracted_watermark)

运行这个代码目录中自动提取出了水印文件。
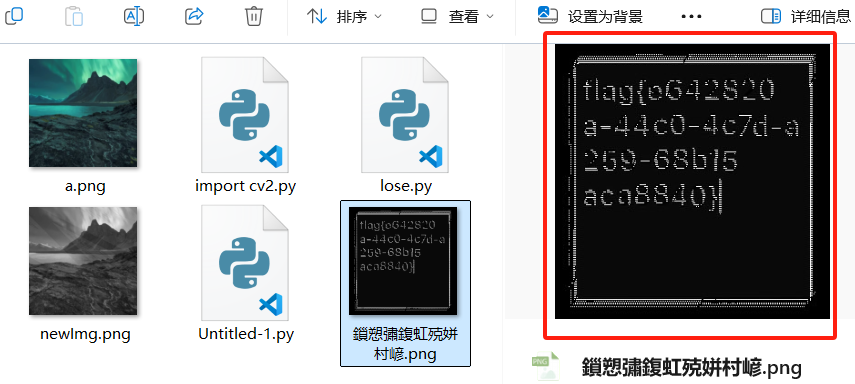得出flag

Reverse逆向RC4

题目

RC4是一种流加密算法，密钥长度可变，它加解密使用相同的密钥，因此也属于对称加密算法。

题目界面

一个可执行文件。

题解

打不开这个可执行文件。是一道逆向的题。我们先去die里面查是多少位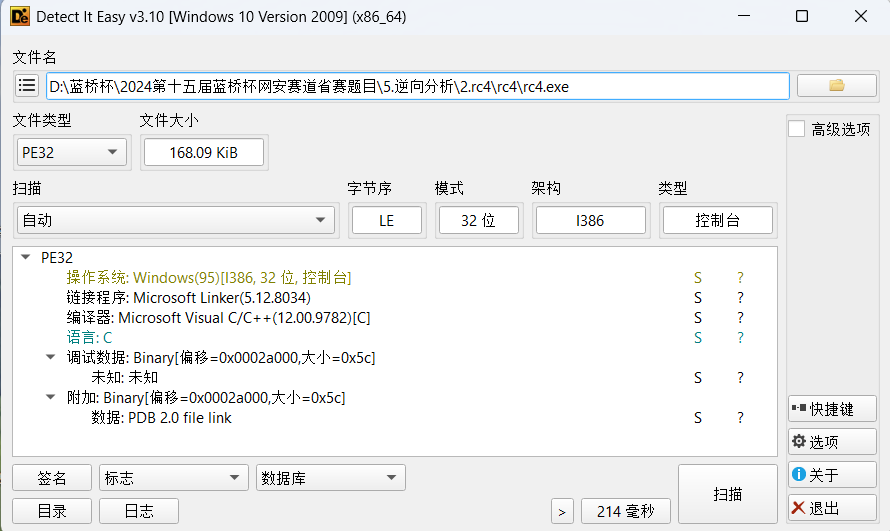，,知道了是32位的程序，我们直接拖进ide32中查壳。
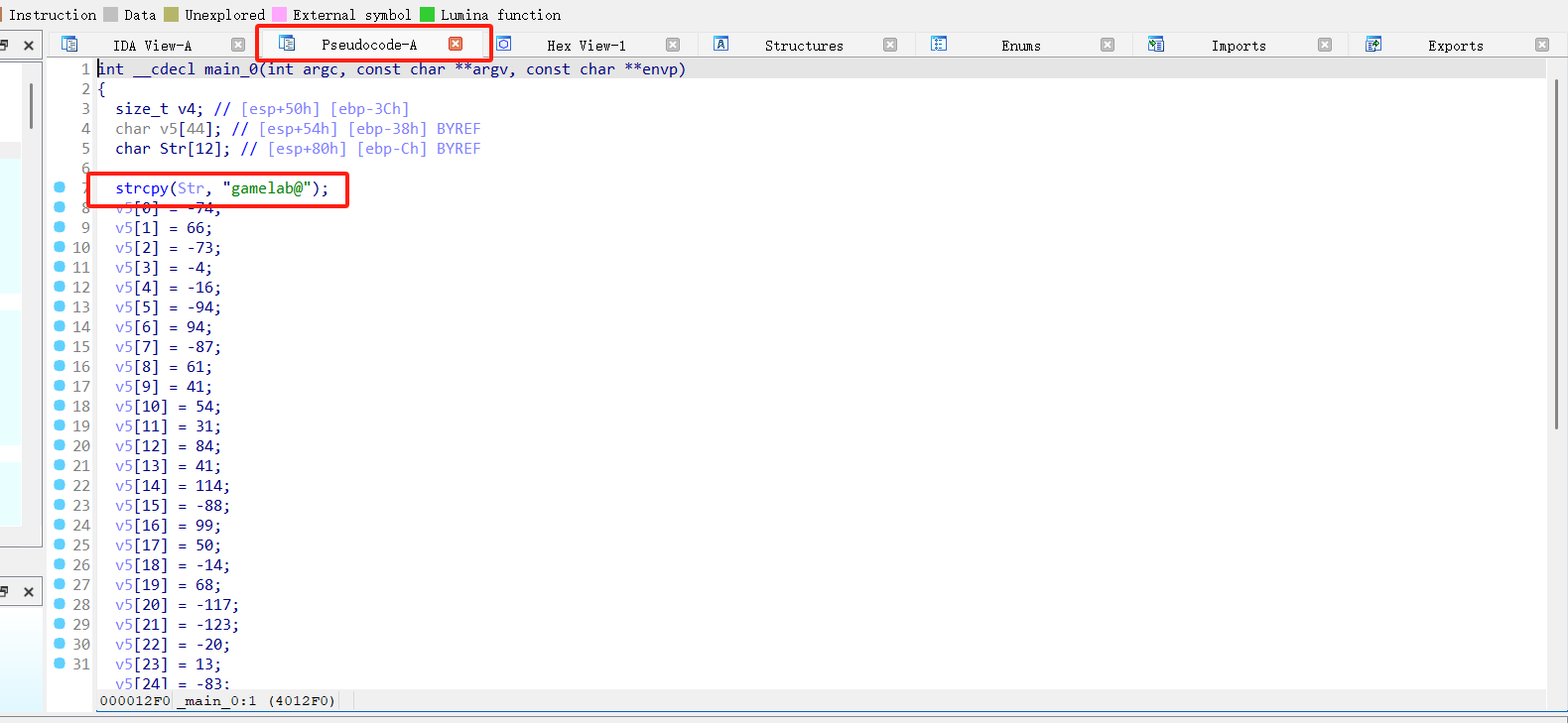把这个程序拖进ida-32位中，然后f5快捷键生成伪代码。
可知为RC4加密，分析程序，猜测Str为密码，v5为密文，将v5转为unsigned char后利用脚本解密可得flag
这段信息是在描述如何使用RC4算法解密一个密文。根据描述，Str变量是RC4算法使用的密钥，而v5数组包含了加密后的密文。解密过程需要将v5数组中的值转换为unsigned char类型，然后使用RC4算法进行解密。

以下是详细的步骤：

1. 理解RC4算法：
   RC4算法是一种流加密算法，它使用一个密钥来初始化一个伪随机数生成器，然后生成一个密钥流，该密钥流与明文进行异或操作以产生密文。解密过程是加密过程的逆过程，即用相同的密钥流与密文进行异或操作以恢复明文。

2. 转换v5数组：
   v5数组中的值是char类型的，可能包含负数。在C语言中，char类型是有符号的，而unsigned char类型是无符号的。因此，需要将v5数组中的值转换为unsigned char类型。在C语言中，这可以通过简单的类型转换实现：

   unsigned char v5_unsigned[44];
   for (int i = 0; i < 44; i++) {
       v5_unsigned[i] = (unsigned char)v5[i] & 0xFF;
   }
   

   这里使用& 0xFF来确保转换后的值在unsigned char的范围内（0-255）。

3. 编写RC4解密脚本：
   使用Python或其他编程语言编写一个RC4解密脚本。以下是一个简单的Python示例，展示如何使用RC4算法进行解密：

   def rc4_decrypt(key, encrypted_data):
       key_length = len(key)
       key_stream = list(range(256))
       x = 0
       y = 0
       for i in range(256):
           x = (x + key_stream[i] + key[i % key_length]) % 256
           key_stream[i], key_stream[x] = key_stream[x], key_stream[i]
   
       x = 0
       y = 0
       decrypted_data = []
       for i in range(len(encrypted_data)):
           x = (x + 1) % 256
           y = (y + key_stream[x]) % 256
           key_stream[x], key_stream[y] = key_stream[y], key_stream[x]
           decrypted_byte = (encrypted_data[i] ^ key_stream[(key_stream[x] + key_stream[y]) % 256]) & 0xFF
           decrypted_data.append(decrypted_byte)
   
       return bytes(decrypted_data)
   
   # 示例密钥和加密数据
   key = b"gamelab@"
   encrypted_data = [-74, 66, -73, -4, -16, -94, 94, -87, 61, 41, 54, 31, 84, 41, 114, -88, 99, 50, -14, 68, -117, -123, -20, 13, -83]
   
   decrypted_data = rc4_decrypt(key, encrypted_data)
   print(decrypted_data.decode())
   

   在这个脚本中，key是RC4算法使用的密钥，encrypted_data是加密后的密文。rc4_decrypt函数实现了RC4解密算法，decrypted_data是解密后的明文。

4. 运行解密脚本：
   将转换后的v5数组值替换到脚本中的encrypted_data变量中，然后运行脚本，查看解密结果。

通过以上步骤，你可以将v5数组中的值转换为unsigned char类型，并使用RC4算法进行解密，从而得到flag。

import base64
def rc4_main(key = "init_key", message = "init_message"):
    print("RC4解密主函数调用成功")
    print('\n')
    s_box = rc4_init_sbox(key)
    crypt = rc4_excrypt(message, s_box)
    return crypt
def rc4_init_sbox(key):
    s_box = list(range(256))
    print("原来的 s 盒：%s" % s_box)
    print('\n')
    j = 0
    for i in range(256):
        j = (j + s_box[i] + ord(key[i % len(key)])) % 256
        s_box[i], s_box[j] = s_box[j], s_box[i]
    print("混乱后的 s 盒：%s"% s_box)
    print('\n')
    return s_box
def rc4_excrypt(plain, box):
    print("调用解密程序成功。")
    print('\n')
    plain = base64.b64decode(plain.encode('utf-8'))
    plain = bytes.decode(plain)
    res = []
    i = j = 0
    for s in plain:
        i = (i + 1) % 256
        j = (j + box[i]) % 256
        box[i], box[j] = box[j], box[i]
        t = (box[i] + box[j]) % 256
        k = box[t]
        res.append(chr(ord(s) ^ k))
    print("res用于解密字符串，解密后是：%res" %res)
    print('\n')
    cipher = "".join(res)
    print("解密后的字符串是：%s" %cipher)
    print('\n')
    print("解密后的输出(没经过任何编码):")
    print('\n')
    return cipher
a=[182,66,183,252,240,162,94,169,61,41,54,31,84,41,114,168,99,50,242,68,139,133,236,13,173,63,147,163,146,116,129,101,105,236,228,57,133,169,202,175,178,198] #cipher
key="gamelab@"
s=""
for i in a:
    s+=chr(i)
s=str(base64.b64encode(s.encode('utf-8')), 'utf-8')
rc4_main(key, s)

用以上python脚本方可解密出flag。flag{12601b2b-2f1e-468a-ae43-92391ff76ef3}

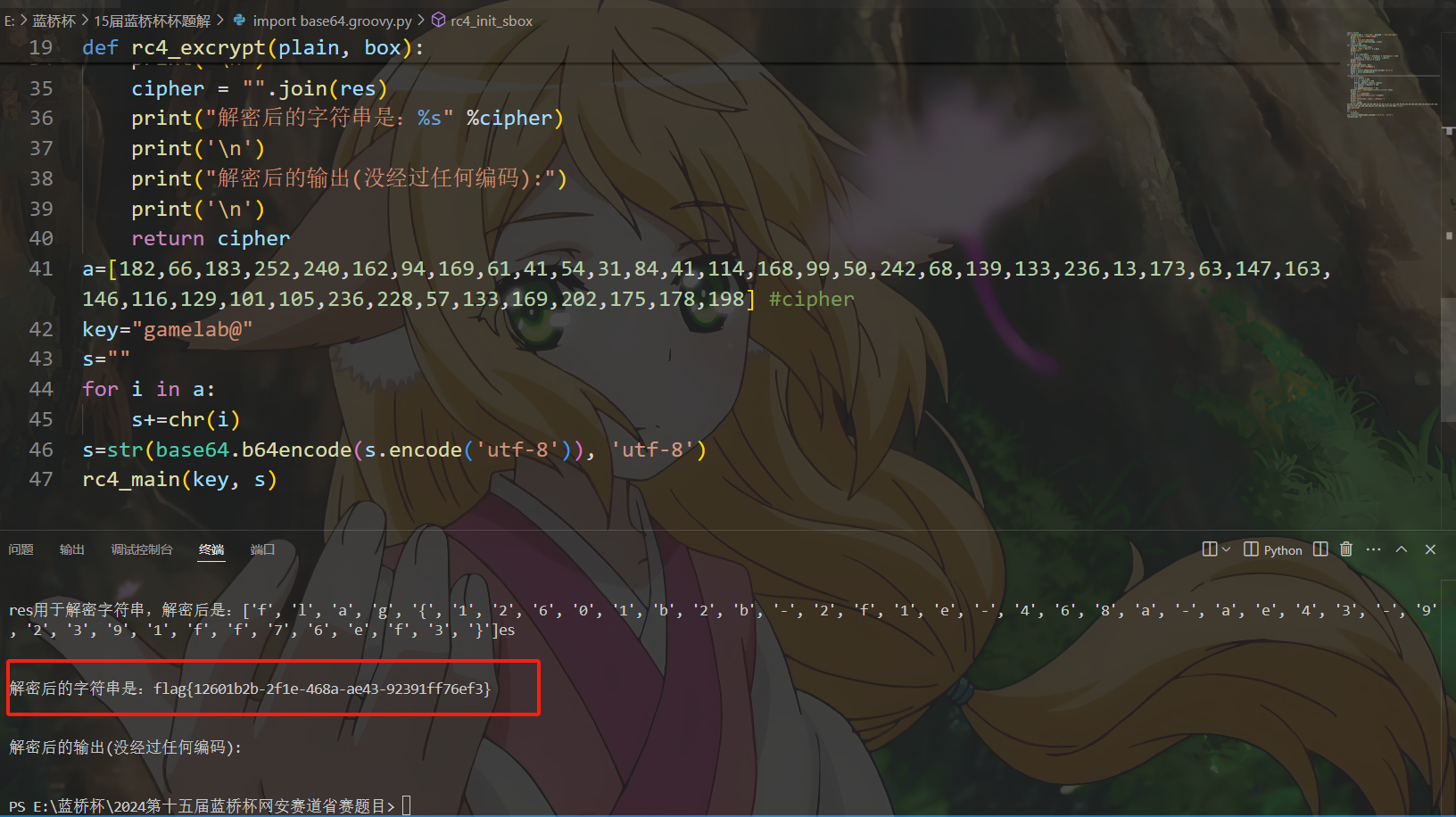
这道题是逆向的签到题，但是逆向对于我还是有点难。然后我也没有啥python基础，这个脚本是我从博客园里面复制过来的。还是有点力不从心，但是我会努力的。
这段代码是一个使用RC4算法进行解密的Python脚本。它包含三个主要函数：rc4_main、rc4_init_sbox和rc4_excrypt。下面是对这段代码的审计和分析：

1. rc4_main 函数

这个函数是主函数，负责调用其他两个函数来完成解密过程。

• 它接受两个参数：key（密钥）和message（待解密的消息）。
• 首先，它调用rc4_init_sbox函数初始化S-box。
• 然后，它调用rc4_excrypt函数进行解密。
• 返回解密后的字符串。

2. rc4_init_sbox 函数

这个函数用于初始化S-box。

• 它接受一个参数：key（密钥）。
• 创建一个从0到255的列表s_box。
• 使用密钥对s_box进行混淆，生成RC4算法所需的S-box。
• 返回混淆后的S-box。

3. rc4_excrypt 函数

这个函数执行RC4解密。

• 它接受两个参数：plain（待解密的密文）和box（S-box）。
• 首先，它尝试对输入的密文进行Base64解码。
• 然后，它使用RC4算法对密文进行解密。
• 解密过程中，它打印出解密的中间结果和最终结果。
• 返回解密后的字符串。

代码问题和改进建议：

1. Base64编码/解码：

   • 在rc4_excrypt函数中，对输入的密文进行Base64解码是不必要的，因为RC4算法直接对字节流进行操作，不需要Base64编码或解码。这可能是一个误解或错误。

2. 打印语句：

   • 代码中包含多个打印语句，这在实际应用中可能不是最佳实践。建议将这些打印语句替换为日志记录，或者在调试完成后删除它们。

3. 错误处理：

   • 代码中没有错误处理机制。例如，如果Base64解码失败，程序可能会抛出异常。建议添加异常处理来提高代码的健壮性。

4. 代码优化：

   • 在rc4_excrypt函数中，bytes.decode(plain)是不必要的，因为plain已经是字节类型。可以直接使用plain。

5. 安全性：

   • RC4算法已经被认为不安全，特别是在某些实现中。如果可能，建议使用更安全的加密算法，如AES。
     这啥问的ai对代码的审计，可以参考参考

ECDSA椭圆曲线数字签名算法

题目

椭圆曲线数字签名算法，它利用椭圆曲线密码学（ECC）对数字签名算法（DSA）进行模拟，其安全性基于椭圆曲线离散对数问题。但是当某些数值相同时会出现一些安全问题。

题目界面

解压task.zip压缩文件。里面有task.py脚本文件和_MACOSX文件夹，文件夹里面有._task.py脚本文件
task.py文件如下

import ecdsa
import random

def ecdsa_test(dA,k):

    sk = ecdsa.SigningKey.from_secret_exponent(
        secexp=dA,
        curve=ecdsa.SECP256k1
    )
    sig1 = sk.sign(data=b'Hi.', k=k).hex()
    sig2 = sk.sign(data=b'hello.', k=k).hex()

    r1 = int(sig1[:64], 16)
    s1 = int(sig1[64:], 16)
    s2 = int(sig2[64:], 16)
    return r1,s1,s2

if __name__ == '__main__':
    n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
    a = random.randint(0,n)
    flag = 'flag{' + str(a) + "}"
    b = random.randint(0,n)
    print(ecdsa_test(a,b))

# (4690192503304946823926998585663150874421527890534303129755098666293734606680, 111157363347893999914897601390136910031659525525419989250638426589503279490788, 74486305819584508240056247318325239805160339288252987178597122489325719901254)

._task.py

选择仍然打开后

题解

task.py脚本文件的代码分析
这段代码使用了ecdsa库来进行椭圆曲线数字签名算法（ECDSA）的签名操作。代码中定义了一个ecdsa_test函数，该函数接受两个参数：dA（私钥）和k（随机数），然后使用这两个参数生成两个签名，并返回签名中的r和s值。下面是对这段代码的审计：

代码分析

1. 私钥和随机数生成：

   • dA是通过random.randint(0, n)随机生成的私钥，其中n是SECP256k1曲线的阶。
   • k也是通过random.randint(0, n)随机生成的随机数。

2. 签名操作：

   • 使用ecdsa.SigningKey.from_secret_exponent创建签名密钥。
   • 使用sk.sign方法对两个不同的消息（b'Hi.'和b'hello.'）进行签名。
   • 签名结果被转换为十六进制字符串，并从中提取出r和s值。

3. 输出：

   • 函数返回两个签名的r和s值。

安全性问题

1. 重复使用随机数k：

   • 在ECDSA中，随机数k应该为每个签名都是唯一的。如果k被重复使用，那么就会泄露私钥信息。这是因为如果两个不同的哈希值e1和e2对应的签名(r1, s1)和(r2, s2)使用了相同的k，则可以通过以下等式推导出私钥dA：
     [
     dA = (s1 - s2) \cdot (z1 - z2)^{-1} \mod n
     ]
     其中，z1和z2是消息的哈希值（在这个例子中，z1和z2是不同的，因为消息不同）。

2. 私钥泄露风险：

   • 由于k被重复使用，攻击者可以通过观察两个签名来计算出私钥dA。一旦私钥泄露，攻击者就可以生成有效的签名，这可能导致严重的安全问题。

改进建议

1. 确保随机数唯一：

   • 对于每个签名操作，都应该生成一个新的随机数k。可以使用ecdsa库的自动随机数生成功能，或者确保每次调用sign方法时都传入一个新的随机数。

2. 代码重构：

   • 避免在签名函数中手动处理签名的生成和解析。使用ecdsa库提供的高级接口来简化代码并减少出错的可能性。
     编写解题脚本

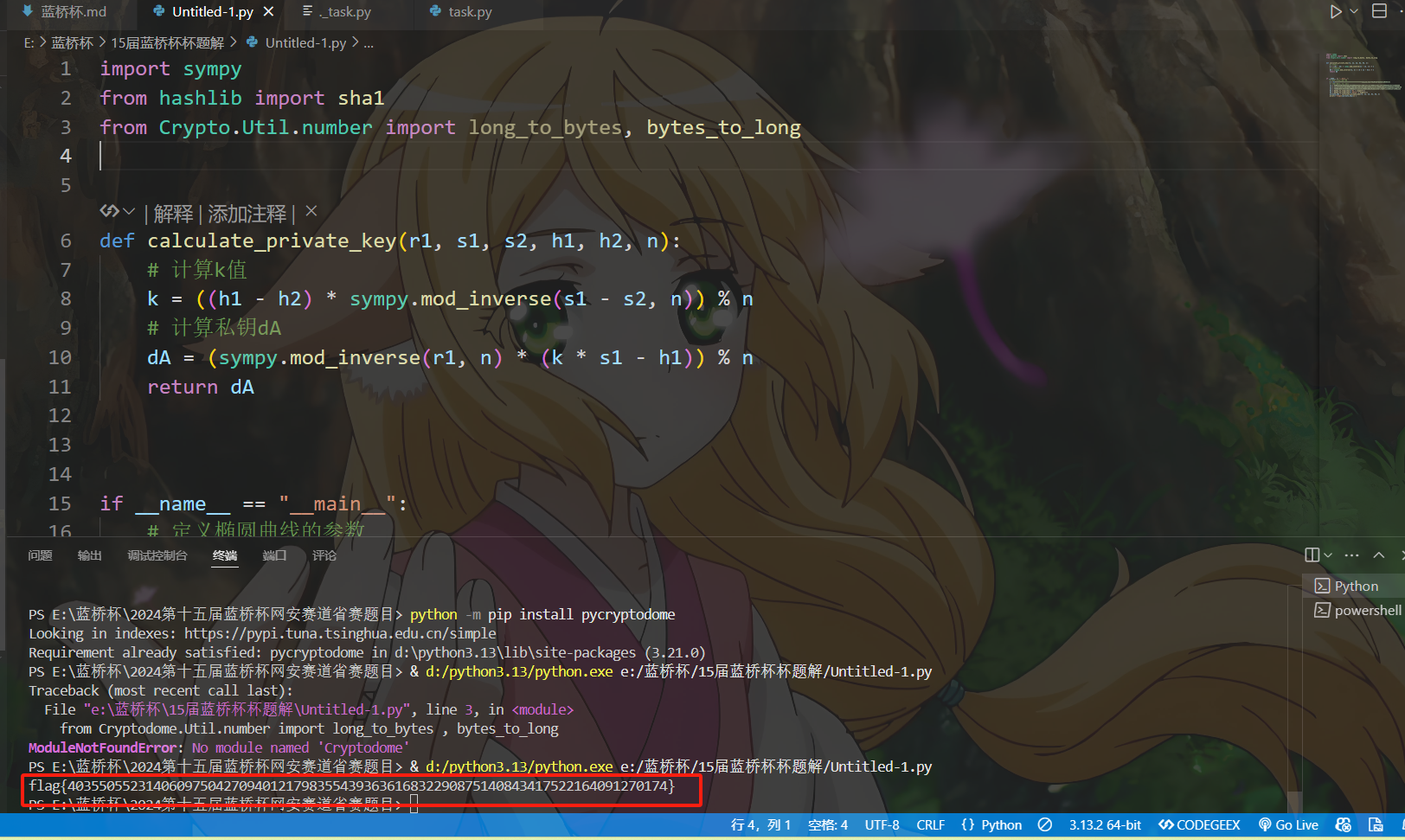
import sympy 
from hashlib import sha1
from Crypto.Util.number import long_to_bytes, bytes_to_long
 
 
def calculate_private_key(r1, s1, s2, h1, h2, n):
    # 计算k值
    k = ((h1 - h2) * sympy.mod_inverse(s1 - s2, n)) % n
    # 计算私钥dA
    dA = (sympy.mod_inverse(r1, n) * (k * s1 - h1)) % n
    return dA
 
 
 
if __name__ == "__main__":
    # 定义椭圆曲线的参数
    n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
    # 签名中的r1, s1, s2值
    r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
    s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788
    s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254
    h1 = bytes_to_long(sha1(b'Hi.').digest())
    h2 = bytes_to_long(sha1(b'hello.').digest())
    private_key = calculate_private_key(r1, s1, s2, h1, h2, n)
    print(f'flag{{{private_key}}}')

这段代码旨在利用ECDSA（椭圆曲线数字签名算法）中的一个弱点来计算私钥。它使用了两个不同的签名（但使用了相同的随机数k），并尝试从这些签名中恢复出私钥。以下是对代码的审计：

代码分析

1. 导入模块：

   • sympy：用于数学运算，特别是求模逆运算。
   • hashlib：用于计算SHA-1哈希值。
   • Crypto.Util.number：用于将长整数转换为字节串，以及将字节串转换为长整数。

2. 函数calculate_private_key：

   • 接受签名中的r1, s1, s2值和两个消息的哈希值h1, h2，以及椭圆曲线的阶n。
   • 计算k值，这是通过(h1 - h2) * sympy.mod_inverse(s1 - s2, n) % n得到的。
   • 计算私钥dA，这是通过(sympy.mod_inverse(r1, n) * (k * s1 - h1)) % n得到的。

3. 主程序：

   • 定义椭圆曲线的参数n。
   • 提供签名中的r1, s1, s2值。
   • 计算两个不同消息的哈希值h1, h2。
   • 调用calculate_private_key函数计算私钥。
   • 打印出私钥。

安全性问题

1. 重复使用随机数k：

   • 代码假设两个签名使用了相同的随机数k。这是ECDSA的一个已知弱点，如果两个签名使用了相同的k，那么私钥可以被计算出来。这在实际应用中应该是避免的，因为随机数k应该是唯一的。

2. 使用SHA-1：

   • 代码使用了SHA-1哈希函数。SHA-1已经被证明是不安全的，应该避免在新的应用中使用。建议使用更安全的哈希函数，如SHA-256。

改进建议

1. 避免重复使用随机数k：

   • 在实际应用中，确保每个签名都使用一个唯一的随机数k。

2. 使用更安全的哈希函数：

   • 替换SHA-1为更安全的哈希函数，如SHA-256。

3. 代码优化：

   • 代码中的计算可以优化，以提高效率和可读性。

4. 错误处理：

   • 添加错误处理，以处理可能出现的异常情况，例如模逆不存在。

5. 代码注释：

   • 添加更多的注释，以解释代码的工作原理和每个步骤的目的。
     

Reverse逆向xxtea

题目

flag被使用了算法分成若干个小块，每个块使用相同的加密解密方法，但是这个算法是对称加密，请将分析密文并还原。

题目界面

题解

做逆向的题，先去die里面查壳，看是几位的。
查出来是64位的。拖进ida-64位查看伪代码。
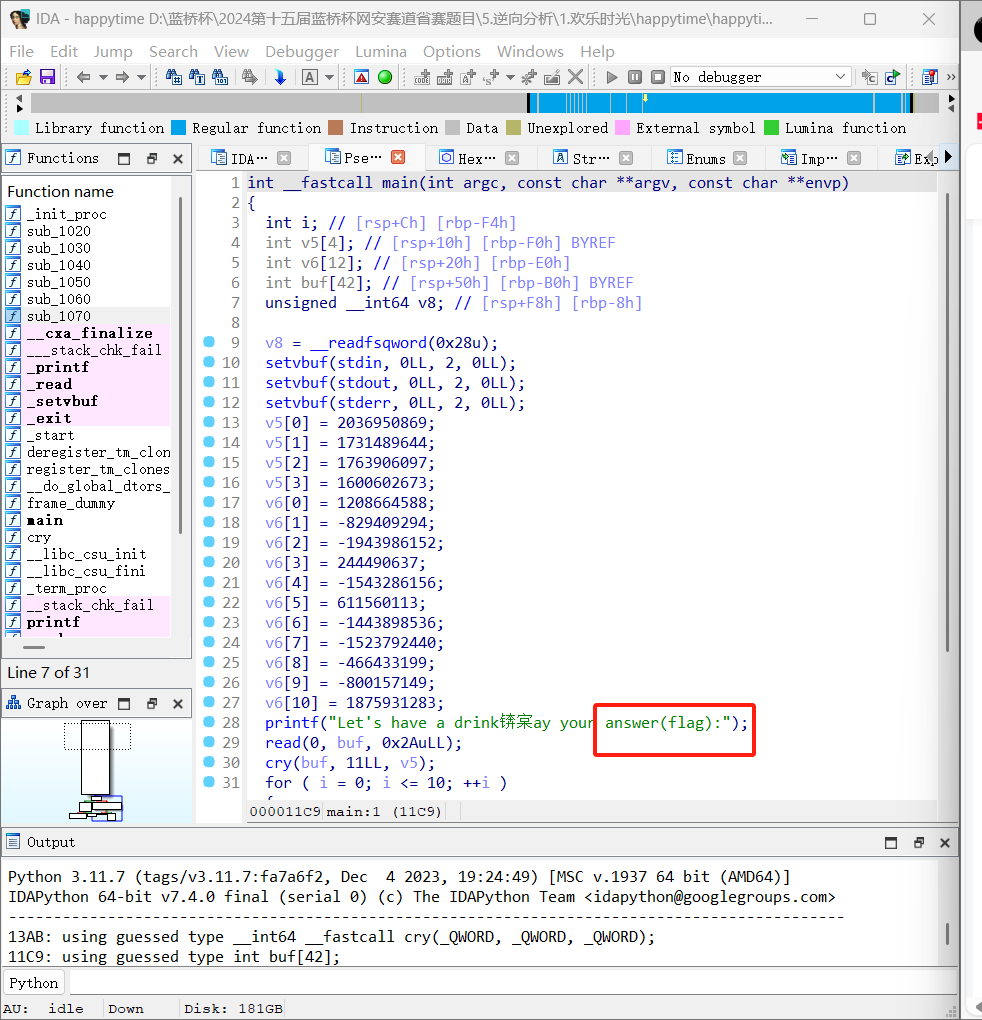好好好，有flag的线索了。
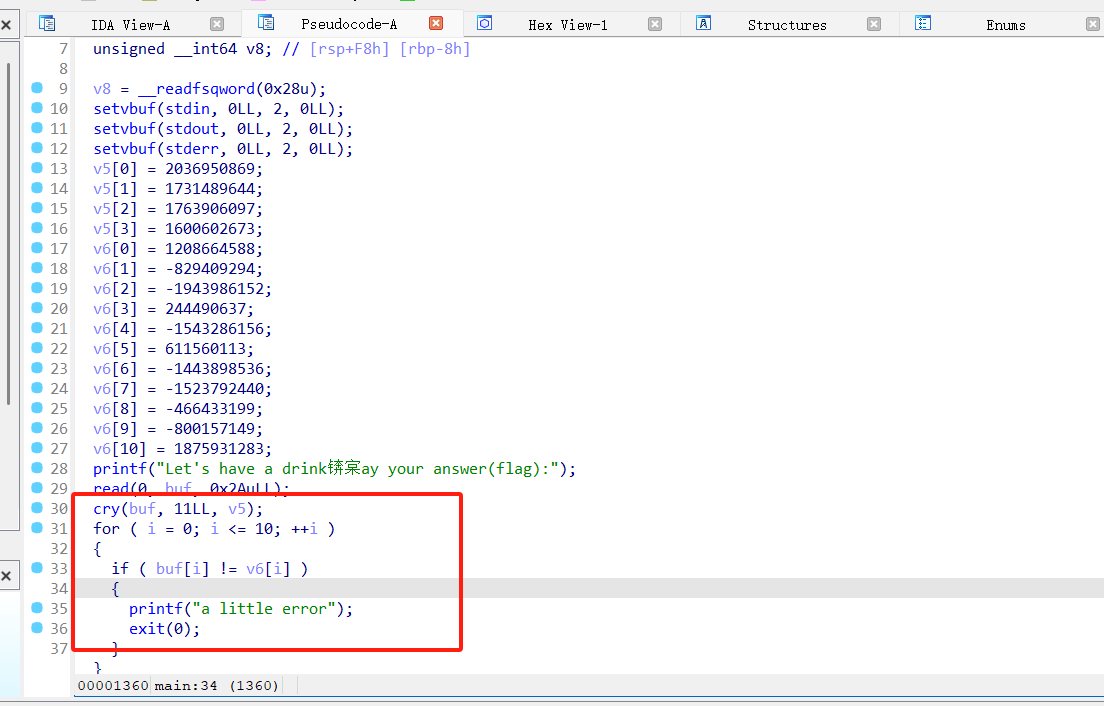主要的函数
伪代码

int __fastcall main(int argc, const char **argv, const char **envp)
{
  int i; // [rsp+Ch] [rbp-F4h]
  int v5[4]; // [rsp+10h] [rbp-F0h] BYREF
  int v6[12]; // [rsp+20h] [rbp-E0h]
  int buf[42]; // [rsp+50h] [rbp-B0h] BYREF
  unsigned __int64 v8; // [rsp+F8h] [rbp-8h]

  v8 = __readfsqword(0x28u);
  setvbuf(stdin, 0LL, 2, 0LL);
  setvbuf(stdout, 0LL, 2, 0LL);
  setvbuf(stderr, 0LL, 2, 0LL);
  v5[0] = 2036950869;
  v5[1] = 1731489644;
  v5[2] = 1763906097;
  v5[3] = 1600602673;
  v6[0] = 1208664588;
  v6[1] = -829409294;
  v6[2] = -1943986152;
  v6[3] = 244490637;
  v6[4] = -1543286156;
  v6[5] = 611560113;
  v6[6] = -1443898536;
  v6[7] = -1523792440;
  v6[8] = -466433199;
  v6[9] = -800157149;
  v6[10] = 1875931283;
  printf("Let's have a drink锛宲ay your answer(flag):");
  read(0, buf, 0x2AuLL);
  cry(buf, 11LL, v5);
  for ( i = 0; i <= 10; ++i )
  {
    if ( buf[i] != v6[i] )
    {
      printf("a little error");
      exit(0);
    }
  }
  printf("yeah,this cup will definitely make you feel better!");
  return 0;
}

代码分析：

这段代码是一个C语言编写的程序，它使用了一个名为 cry 的函数来处理用户输入的 flag。以下是对代码的审计：

代码分析

1. 变量声明：

   • v5[4]：一个包含4个整数的数组，可能用作加密函数的密钥或其他参数。
   • v6[12]：一个包含12个整数的数组，可能包含加密后的预期结果或用于验证的数据。
   • buf[42]：一个较大的数组，用于存储用户输入的数据。
   • v8：一个无符号64位整数，用于存储文件流缓冲区的初始状态。

2. 文件流缓冲区设置：

   • 使用 setvbuf 函数设置 stdin、stdout 和 stderr 的缓冲区为无缓冲（2 表示不缓冲）。

3. 数组初始化：

   • v5 和 v6 数组被初始化为特定的整数值。

4. 用户输入：

   • 使用 printf 输出提示信息，要求用户输入 flag。
   • 使用 read 函数从标准输入读取42字节的数据到 buf 数组中。

5. 加密函数调用：

   • 调用 cry 函数处理 buf 数组中的数据，11LL 可能是一个参数，表示处理的数据长度。

6. 验证过程：

   • 通过一个循环比较 buf 数组中的前11个元素与 v6 数组中的元素。如果有任何不匹配，程序输出 "a little error" 并退出。

7. 成功消息：

   • 如果所有元素都匹配，程序输出 "yeah, this cup will definitely make you feel better!"。

安全性问题

1. 缓冲区溢出：

   • read(0, buf, 0x2AuLL); 读取了42字节的数据到 buf 数组中，但没有检查输入是否超过数组的大小。如果用户输入超过42字节，可能会导致缓冲区溢出。

2. 缺乏输入验证：

   • 程序没有验证用户输入的内容，除了长度和与 v6 数组的比较。这可能允许恶意输入。

3. 加密函数的安全性：

   • cry 函数的具体实现未知，如果它不够安全，可能会导致加密过程的弱点。

改进建议

1. 输入验证：

   • 在读取用户输入之前，应该验证输入的长度和内容，以防止缓冲区溢出和其他潜在的安全问题。

2. 安全编码实践：

   • 使用更安全的编码实践，如初始化所有变量，避免使用魔法数字，添加更多的错误处理和日志记录。

3. 加密函数的审计：

   • 对 cry 函数进行审计，确保其实现是安全的，并且没有已知的弱点。

4. 使用安全的输入函数：

   • 考虑使用更安全的输入函数，如 fgets，它允许指定最大读取长度，从而避免缓冲区溢出。

5. 代码注释：

   • 添加更多的注释，以解释代码的工作原理和每个步骤的目的，特别是对于 cry 函数的调用和参数。

通过这些改进，可以提高代码的安全性和健壮性，减少潜在的安全风险。

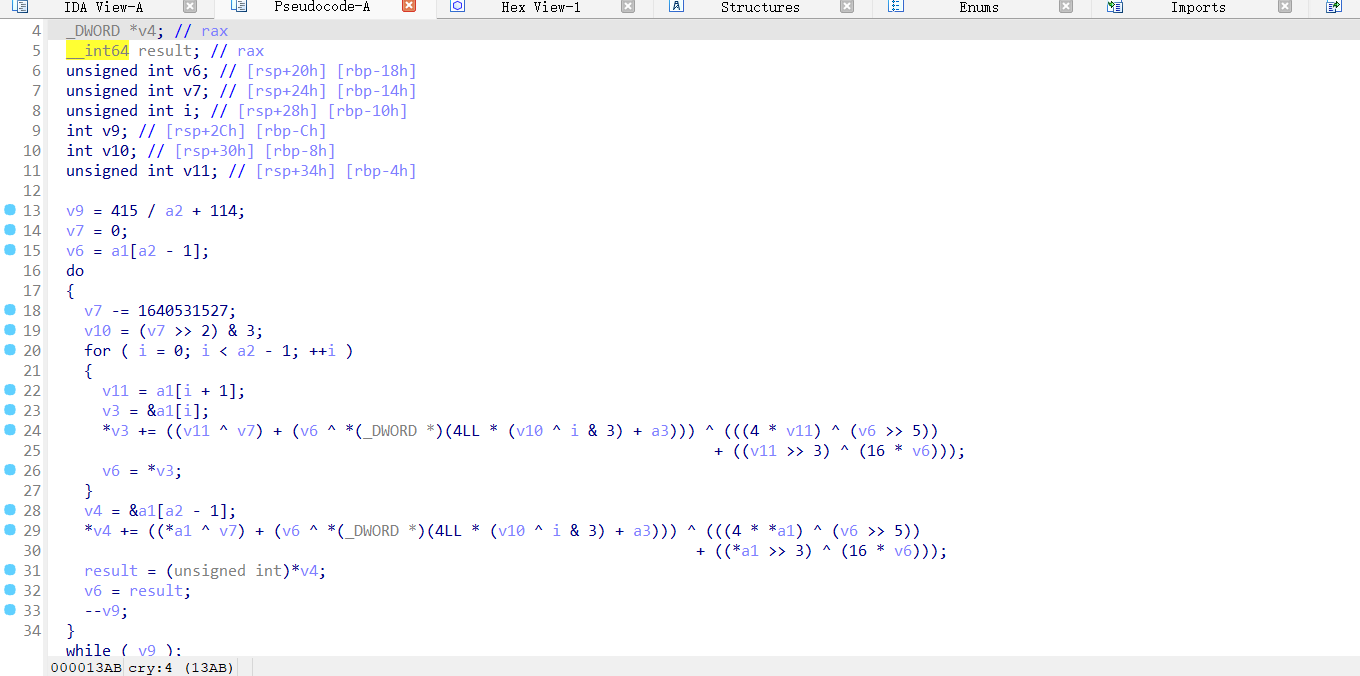
我们看一下cry函数的伪代码的审计
这两段代码展示了一个名为 cry 的函数的实现，这个函数看起来是一个加密或变换函数，它对输入数据进行某种形式的处理。下面是对这些代码的审计：

第一段代码（IDA反汇编代码）

1. 函数签名：

   • __int64 __fastcall cry(__DWORD *a1, int a2, __int64 a3)：这是一个使用 __fastcall 调用约定的函数，接受三个参数：一个指向 DWORD 类型的指针 a1，一个整数 a2，和一个 int64 类型的 a3。

2. 变量声明：

   • 函数内部声明了多个变量，包括指针、整数和无符号整数。

3. 初始化：

   • v9 被初始化为 415 / a2 + 114，这可能是一个循环计数器。
   • v7 被初始化为 0，可能用作循环中的累加器或状态变量。
   • v6 被初始化为 a1[a2 - 1]，这可能是获取输入数组的最后一个元素。

4. 循环结构：

   • 函数包含一个 do-while 循环，其中包含一个 for 循环。这些循环可能用于对输入数据进行多次处理。

5. 数据处理：

   • 在循环中，函数对 a1 数组中的元素进行复杂的位操作和算术运算。这些操作可能涉及到加密算法的某个步骤。

6. 返回值：

   • 函数返回 result，这是对输入数据处理后的结果。

第二段代码（C代码）

1. 函数签名：

   • int64 _fastcall cry(DWORD*a1, int a2, int64 a3)：与第一段代码相同，这是一个使用 __fastcall 调用约定的函数。

2. 变量声明：

   • 与第一段代码类似，函数内部声明了多个变量。

3. 初始化：

   • v9、v7 和 v6 的初始化与第一段代码相同。

4. 循环结构：

   • 包含一个 do-while 循环，其中包含一个 for 循环。

5. 数据处理：

   • 在循环中，函数对 a1 数组中的元素进行复杂的位操作和算术运算。这些操作与第一段代码中的操作相似。

6. 返回值：

   • 函数返回 result，这是对输入数据处理后的结果。

安全性问题

1. 缓冲区溢出：

   • 如果 a2 的值过大，可能会导致对 a1 数组的访问超出其边界，从而引发缓冲区溢出。

2. 未初始化的变量：

   • 一些变量（如 v3、v4）在使用前可能未被正确初始化，这可能导致未定义行为。

3. 复杂的位操作：

   • 函数中的位操作和算术运算非常复杂，可能难以理解和维护。这可能隐藏潜在的安全漏洞。

改进建议

1. 输入验证：

   • 在处理输入数据之前，验证 a2 的值，确保它不会超过 a1 数组的大小。

2. 初始化所有变量：

   • 确保所有变量在使用前都被正确初始化。

3. 简化代码：

   • 尝试简化复杂的位操作和算术运算，使其更易于理解和维护。

4. 代码注释：

   • 添加更多的注释，解释每个步骤的目的和逻辑，特别是对于复杂的位操作和算术运算。

5. 使用安全的编码实践：

   • 使用更安全的编码实践，如避免使用魔法数字，添加更多的错误处理和日志记录。

通过这些改进，可以提高代码的安全性和健壮性，减少潜在的安全风险。
然后编写一个脚本解密。

from ctypes import *


def MX(z, y, total, key, p, e):
    temp1 = (z.value>>5 ^ y.value<<2) + (y.value>>3 ^ z.value<<4)
    temp2 = (total.value ^ y.value) + (key[(p&3) ^ e.value] ^ z.value)
    
    return c_uint32(temp1 ^ temp2)


def decrypt(n, v, key):
    delta = 0x61C88647
    rounds = int((415 / n) + 114) # 魔改的位置1
    
    total = c_uint32(0 - rounds * delta) # 魔改的位置2
    y = c_uint32(v[0])
    e = c_uint32(0)

    while rounds > 0:
        e.value = (total.value >> 2) & 3
        for p in range(n-1, 0, -1):
            z = c_uint32(v[p-1])
            v[p] = c_uint32((v[p] - MX(z,y,total,key,p,e).value)).value
            y.value = v[p]
        z = c_uint32(v[n-1])  
        v[0] = c_uint32(v[0] - MX(z,y,total,key,0,e).value).value
        y.value = v[0]  
        total.value += delta # 魔改的位置3
        rounds -= 1

    return v 


if __name__ == "__main__":
    v = [0x480AC20C, 0xCE9037F2, 0x8C212018, 0x0E92A18D, 0xA4035274, 0x2473AAB1, 0xA9EFDB58, 0xA52CC5C8, 0xE432CB51, 0xD04E9223, 0x6FD07093]
    k = [0x79696755, 0x67346F6C, 0x69231231, 0x5F674231]
    n = 11 # 魔改的位置4

    res = decrypt(n, v, k)
    for i in res:
        print(str(i.to_bytes(4, 'little'))[2:-1], end='')

这段Python代码实现了一个简单的解密算法，它似乎是为了逆转一个特定的加密过程。代码由两个主要函数组成：MX 和 decrypt，以及一个执行解密并打印结果的主程序部分。

函数 MX

• 这是一个辅助函数，用于执行解密过程中的核心计算。
• 它接受六个参数：z、y、total、key、p 和 e，其中 z 和 y 是 c_uint32 类型的变量，代表正在处理的数据；total 是一个累加器，用于跟踪解密状态；key 是一个密钥列表，用于提供加密过程中的随机性；p 是当前处理的数据块索引；e 是一个临时变量，用于计算。
• 函数内部首先计算两个临时值 temp1 和 temp2，它们是输入参数的一系列位运算的结果。
• 最后，函数返回 temp1 和 temp2 的异或结果，这个结果将用于更新解密过程中的数据块。

函数 decrypt

• 这是主要的解密函数，它接受三个参数：n（数据块的数量）、v（一个包含加密数据的列表）和 key（密钥列表）。
• 函数首先计算解密轮数 rounds，这个值取决于数据块的数量 n。
• 然后，初始化 total 为一个基于 rounds 和 delta（一个魔术数字）的值，y 为列表 v 的第一个元素，e 为 0。
• 接下来，函数进入一个 while 循环，直到 rounds 为 0。在每次循环中，它更新 e 的值，然后反向遍历 v 列表，使用 MX 函数更新每个数据块的值，并更新 y 的值。
• 在每轮循环的最后，更新 total 的值并减少 rounds。
• 函数返回解密后的数据块列表 v。

主程序

• 在 if __name__ == "__main__": 块中，定义了加密数据 v 和密钥 k。
• 调用 decrypt 函数进行解密，并将结果存储在 res 中。
• 最后，程序遍历解密后的结果 res，将每个 uint32 值转换为字节串，并打印出来。这里使用了 to_bytes(4, 'little') 方法将整数转换为4字节的小端字节串，然后使用字符串切片 [2:-1] 去除字节串的前缀 b' 和后缀 '，最后使用 end='' 参数确保打印的字节串之间没有空格。

总的来说，这段代码的目的是逆转一个特定的加密过程，恢复原始数据。这个过程涉及到复杂的位运算和密钥使用，可能是为了模拟一个简单的加密算法的解密过程。

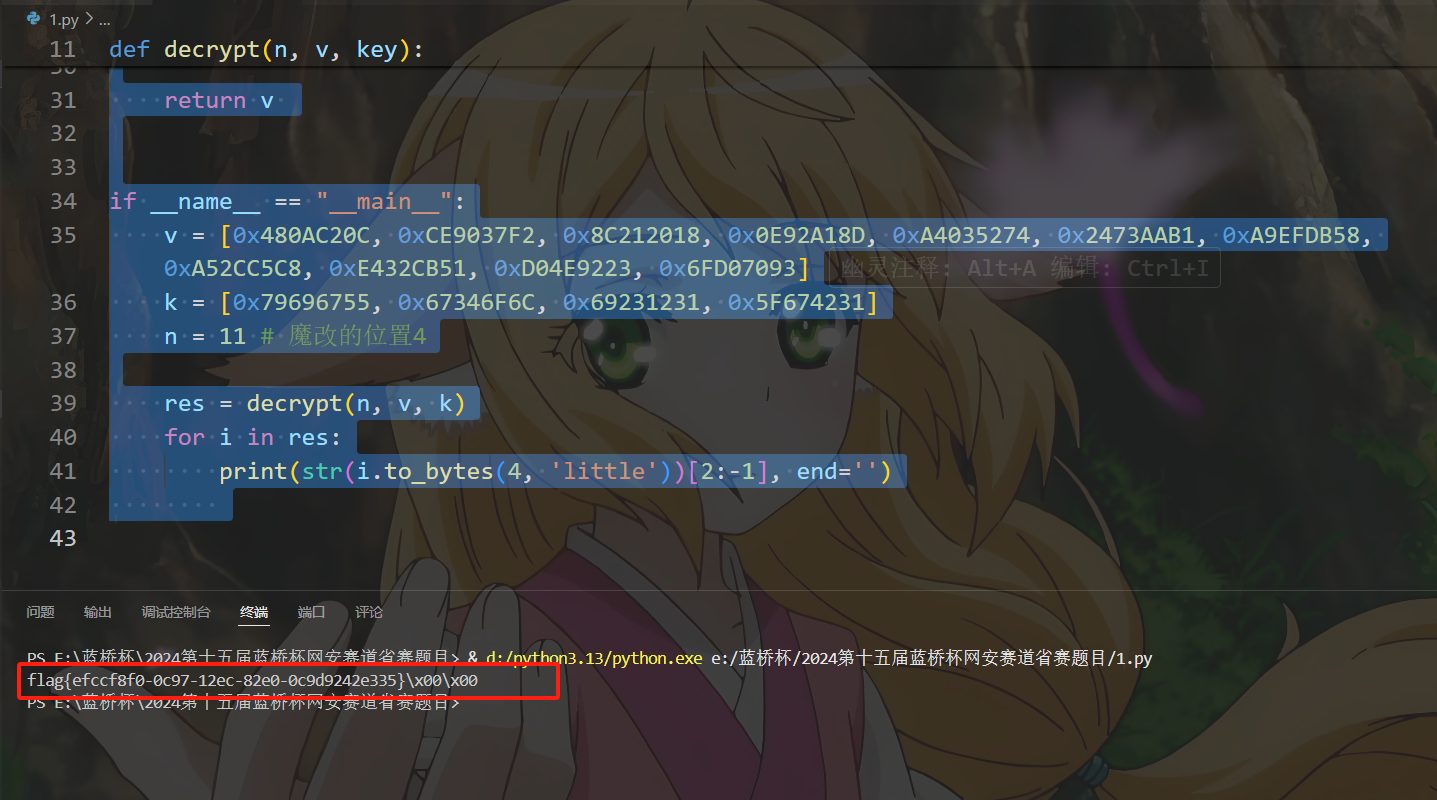得出flag为flag{efccf8f0-0c97-12ec-82e0-0c9d9242e335}